How To Draw Nyquist Plot From Bode

Recently I wrote a post on stability of linear systems where I introduced the Nyquist plot. Now I want to go into the details of how to draw one without using a Bode plot. If I have fourth dimension in the future I will also explain how to draw a Nyquist plot using the Bode plot - it is an easier method, in my stance, just it assumes that you take a reliable Bode plot to start with.

I start want to clarify something from last post: The Caucy Argument Principle states that [3]:

The internet number of clockwise encirclements, N, equals the number of zeros (airtight-loop organization roots) in the RHP, Z, minus the number of open up-loop poles in the RHP, P: N = Z - P

I learned to draw Nyquist plots this mode from Brian Douglas [one], but he references a lecture by Prof. Gopal [2], and so I will cite both here for abyss. We will use an instance transfer office given below, but first I desire to become over ii concepts that will exist useful in this example. The kickoff concept is the thought that Nyquist plots are symmetric most the existent axis (in both the due south- and w-planes) [1]. We will use this to reduce the amount of work we have to exercise to obtain the plot.

The second concept is the idea that the role of the Nyquist profile in the s-plane that is at infinity (i.eastward. the curved part that encircles the entire RHP) maps to a unmarried signal in the west-plane if the transfer part is proper or strictly proper [ane]. This is considering, if we imagine ourselves sitting on this function of the contour, the poles and zeros of the transfer part would appear grouped at a signal well-nigh the origin [1]. That is, no matter where we are at infinity, we would be so far away that we could not run into the contributions of the poles and zeros to the phase. Then we only demand one signal to represent the phase anywhere at infinity on the RHP. If the organization is strictly proper, this point is the origin; if the arrangement is proper, this point is somewhere on the real axis [1]. This also ways that I actually but intendance about what is happening along the imaginary axis in the s-plane [1].

Fig 1
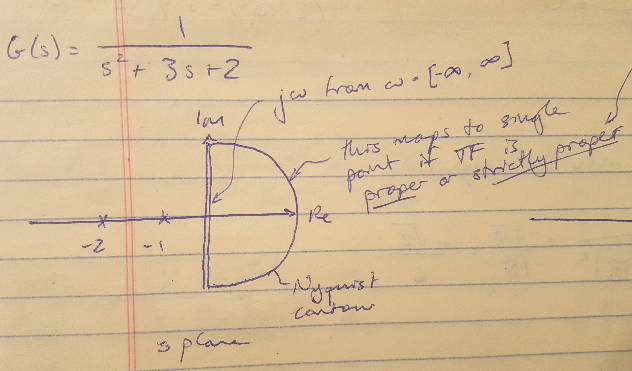
Figure 1

At present allow's dive into the example. The open up loop transfer office is given below [1]. It has no zeros (Z = 0) and two poles in the LHP (P = 0). And so nosotros are expecting that N = Z - P = 0 for this example.

Eqn 1

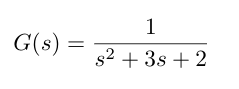
Prof. Gopal'southward method states that you only need four points to be able to sketch the Nyquist plot, and these points are [1],[2]:

(1) w = 0
(2) w = infinity
(3) The intercept of the Nyquist plot (in the w-plane) on the imaginary axis
(4) The intercept of the Nyquist plot (in the westward-aeroplane) on the real axis

In order to get all of these points, we beginning need to substitute southward = jw into the organization transfer function [1]. Why don't I substitute due south = sigma + jw into the transfer function, why am I omitting the existent part? I omit the real function for the reason we just discussed - equally soon equally I move onto the positive real axis at a distance of infinity from the origin, the phase contribution from the transfer function basically looks like zero to me. It's not important to me. And so I tin can omit considerations of the real component of the transfer function completely from this process.

Eqn 2

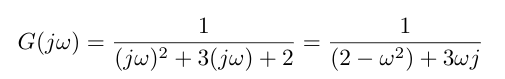
Instead, let's substitute j*west into my transfer function equally shown beneath.

Now let'south come across what happens when westward = 0 - I find that the transfer function is equal to 0.v, and so I plot that on the positive real axis of the w-aeroplane. Similarly, I tin can see that when w = infinity, my transfer function is equal to 0, so I tin also plot that on the w-plane.

Fig 2
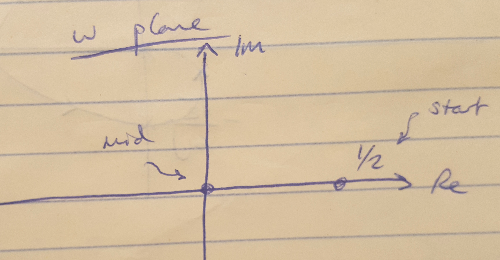
Figure ii

Next we demand to find the imaginary and real centrality intercepts of the Nyquist plot. To do this, I am going to rationalize the denominator of my transfer function and then separate the existent and imaginary components as shown below.

Eqn 3

Eqn 4

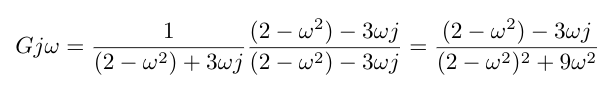
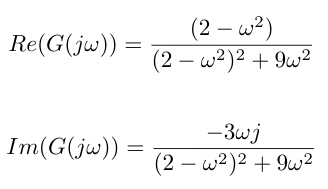
I can solve for the intercept for the imaginary axis by setting the real centrality component equal to nil and solving for w. Then I plug this value of w into the imaginary component to get the imaginary axis intercept. This math is shown beneath, and the final Nyquist plot is also given. Notice that I ever describe my Nyqyuist profile in the southward-plane in the clockwise direction, and so the signal in the w-plane that corresponds to the origin in the s-plane is the starting indicate for my contour, and I move in the direction of the point corresponding to w = infinity in the s-plane [ane].

Eqn 5

Fig 3
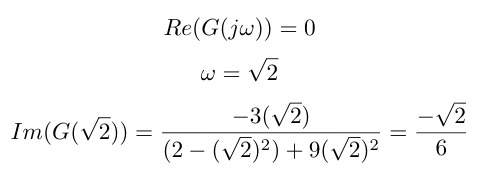
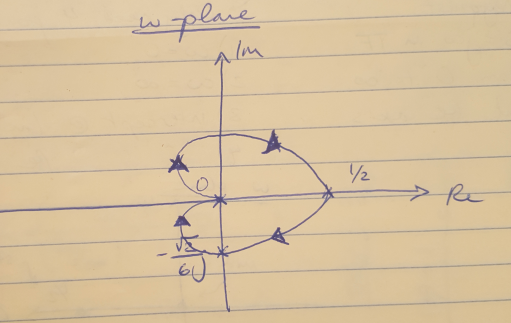
Figure 3

This plot shows that my system is stable because I take no encirclements of -one and N = Z - P = 0 as we expected.

References

[1] Douglas, Brian. "Nyquist Stability Criterion, Part two." https://www.youtube.com/scout?v=tsgOstfoNhk&list=PLUMWjy5jgHK1NC52DXXrriwihVrYZKqjk&index=27 Visited 09/16/2019.

[two] Gopal, Madan. "Lec-36 The Nyquist Stability Criterion and Stability Margins (Contd.)." https://www.youtube.com/watch?5=Rbvau5oXOkg Visited 09/16/2019.

[iii] Franklin, K., Powell, J.D., Emami-Naeini, A. Feedback Control of Dynamic Systems, 6th ed. Pearson. 2009.